哈工大 SCIR 实验室笔试小记
昨天参加了哈工大 SCIR 实验室的 2024 研究生招生笔试。试题很基础,但题量很大,一个半小时要完成一道逻辑题,一道文献翻译题,两道数学题,两道神经网络相关知识的题,两道编程题。反正我没做完。
本文给出两道数学题和两道编程题的题解,权当复习巩固基础。
一、高斯分布的 KL 散度
这道题完全空着了,忘了 KL 散度怎么求了。究其原因是没有深入理解信息熵、交叉熵、相对熵那一套原理 [1]。
信息熵:
交叉熵:
其中,
相对熵(KL 散度):
其实就是衡量交叉熵与信息熵的差值。
KL 散度的若干条性质:
- KL 散度大于等于 0,简单证明:
- 对
,有 ,从而
- 对
- 可以理解为两个分布的距离,但是并不满足对称性和三角不等式
回到本题:
第一项:
第二项要看出里面是方差:
第三项,注意
综上:
二、组合题(图论)
有 n 个人,每次坐成一圈,为了使每次每个人的邻居与之前都不同,则坐法最多有几次?
实际上可以抽象为:完全图
很明显,要将每个人都认识一遍且不重复,不会超过
奇数:
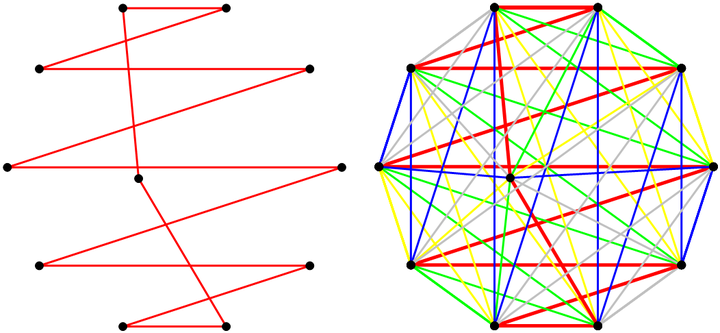
可以旋转
偶数:

可以旋转
故,答案为
三、编程题(求编辑距离)
经典的字符串 dp 题:
int minDistance(string word1, string word2) {
int m = word1.size(), n = word2.size();
vector<vector<int>> dp(m + 1, vector<int>(n + 1));
// dp[i][j] = max(
// dp[i-1][j] + 1, 删除
// dp[i][j-1] + 1, 插入
// dp[i-1][j-1] + 1, 修改
// )
for (int i = 0; i <= m; i++) dp[i][0] = i;
for (int j = 0; j <= n; j++) dp[0][j] = j;
for (int i = 1; i <= m; i++) {
for(int j = 1; j <= n; j++) {
dp[i][j] = min(dp[i-1][j] + 1, dp[i][j-1] + 1);
if (word1[i - 1] == word2[j - 1]) {
dp[i][j] = min(dp[i][j], dp[i-1][j-1]);
}
else {
dp[i][j] = min(dp[i][j], dp[i-1][j-1] + 1);
}
}
}
return dp[m][n];
}
四、编程题(滑动窗口)
主要考虑如果 i > j,并且 nums[i] > nums[j],则 j 就可以丢弃,故维护一个单调队列:
vector<int> maxSlidingWindow(vector<int>& nums, int k) {
int n = nums.size();
deque<int> d;
vector<int> ans;
for(int i = 0; i < n; i++) {
while(!d.empty() && nums[d.back()] <= nums[i]) d.pop_back();
d.push_back(i);
if(i >= k - 1) {
while(!d.empty() && d.front() <= i - k) d.pop_front();
ans.push_back(nums[d.front()]);
}
}
return ans;
}