二维凸包问题详解
这是我在做软件构造实验时遇到的问题,同时,它也是 LeetCode 4 月 23 日的每日一题。我之前没有系统刷过算法,既然遇到了就索性学习并总结一下。题目链接:
什么是凸包?
简单来说,可以想象在平面中有一些点,这些点的集合为

凸包计算有很多办法,我在本文讲解三个做法
Gift wrapping 算法
这是我在做 MIT 6.031-Problem Set 0 时,实验指导建议的做法。由于这门课教授的是软件构造,不太注重时间复杂度,所以这个算法时间性能并不好,使用者寥寥,但是它很直观且很有趣,从它开始入门凸包问题不失为一个好的选择
所谓 Gift wrapping,顾名思义,就是模拟包装礼品盒的过程。要拿包装带给一个礼品盒包装,首先肯定是从凸包中的一个点开始,沿着某一条边后到达下一个顶点,然后从包装带原来的方向开始,逐步向内旋转,直到接触到下一个点,那么下一条边就包装完成了。文字描述有些困难,可以看图:

先包装 AB 边,随后包装带从 AB 方向向内旋转,直到遇到 C 点,则凸包的下一个点就是 C
算法:
- 找到一个一定在凸包中的初始点,比如最左下的点
- 计算剩下的所有点与初始点正向下方向之间的角度,取最小的角度的点加入闭包
- 对于最新加入凸包的点,取前一个点指向该点的方向作为初始方向,遍历剩下的点,取剩下的点和该点的连线与初始方向夹角最小的点加入凸包
- 重复 3,直到找到的下一个点是初始点
最终结果如图:

计算角度
为了达到目的,先实现一个计算角度的函数,根据初始角度,当前点的坐标,以及目标点的坐标,计算初始角度与当前点和目标点连线的夹角
public static double calculateBearingToPoint(double currentBearing, int currentX, int currentY,
int targetX, int targetY) {
double angle = 180*Math.atan2(targetY - currentY, targetX - currentX)/Math.PI;
double bearing;
bearing = 90 - angle - currentBearing;
if(bearing < 0) bearing += 360;
return bearing;
}
这里的角度指的都是从该点正上方逆时针旋转的角度
考虑距离

我们先明确一点:对于上图,A、B、C、D 四点共线,由凸包的定义, A、D 应该在凸包中,B,C 不应该在凸包中
从 A 点开始计算角度,角度最小的有 B,C,D 点,那么显然接下来要选择距 A 点最远的 D 点。所有我们的算法在扩充凸包时,应该计算一下距离,如果有多个点需要旋转的角度均最小且相同,则应选择距离最远的点
完整代码
public static Set<Point> convexHull(Set<Point> points) {
if (points.size() <= 3) return points;
Set<Point> convexHull = new HashSet<>();
Point first = points.iterator().next();
/* 找到最左下边的点,否则如果与起始点同横坐标的点大于等于三,则距离更新的时候,最后永远无法回到起始点 */
for (Point iter : points) {
if (iter.x() < first.x() || (iter.x() == first.x() && iter.y() < first.y()))
first = iter;
}
Point p = first; //当前的最新点
/* pre这样设置的目的是使初始角度为0 */
Point pre = new Point(first.x(), first.y() - 1); //保存前一个点
Point endpoint = p; //待加入集合的点
do {
double minAngle = 360;
double maxDis = 0;
convexHull.add(p);
//System.out.println(p.x() + " " + p.y());
double curBearing = 180 * Math.atan2(p.y() - pre.y(), p.x() - pre.x()) / Math.PI;
//System.out.println((p.y() - pre.y())+ " " + (p.x() - pre.x()) + ":" + curBearing);
/* 计算当前角度 */
if (p.x() >= pre.x()) curBearing = 90 - curBearing;
else if (p.y() > pre.y()) curBearing = 450 - curBearing;
else if (p.y() < pre.y()) curBearing = 90 - curBearing;
//System.out.println(curBearing);
for (Point next : points) {
double curAngle = calculateBearingToPoint(curBearing, (int) p.x(), (int) p.y(), (int) next.x(), (int) next.y());
double curDis = Math.pow(next.x() - p.x(), 2) + Math.pow(next.y() - p.y(), 2);
/* 要确保这个点与之前的点不同,否则可能会死循环
但也要注意可以与第一个点相同,否则循环无法退出 */
if (curAngle < minAngle && next != p) {
endpoint = next;
minAngle = curAngle;
maxDis = curDis;
}
/* 如果有角度相同即共线的,则取最远的点 */
if (curAngle == minAngle && curDis > maxDis && next != p) {
maxDis = curDis;
endpoint = next;
}
}
//System.out.println(minAngle);
pre = p;
p = endpoint;
} while (p != first);
return convexHull;
}
复杂度分析
对于凸包中的每一个点,都要遍历其它所有点,所以该算法的时间复杂度为
由于我这个是按照实验要求写的代码,其中用到了 atan,所以时间性能可能会更差。事实上我们不需要精确计算角度,只需要比较角度的大小关系就可以了,可以用点乘来代替角度的计算
Graham 扫描法
先给出算法:
- 找到一个一定在凸包中的初始点,比如最左下的点
- 按逆时针逐个加入可能在凸包中的点。做法就是先把剩下的点集按照相对初始点的极角排序,如果极角相同,则按距离排序,近的在前(原因后面解释)
- 从初始点开始,按顺序不断加入凸包,对于加入的每一个点,判断加入该点后,会不会使凸包呈现一种前一个点往内凹陷的形状,如果是这样的,则从凸包中删除前一个点,继续往前判断(怎么判断形状呢?利用叉乘)
下面我来详细解释一下算法实现
利用叉乘
对于平面中两个向量
,则 相对于 为顺时针 ,则 相对于 为逆时针 ,则 和 共线
首先,我们可以利用这个办法来实现算法的第 2 步,排序。所谓按极角顺序排序,就是将剩下点集与初始点组成的向量按逆时针排列,对其中两个向量做叉乘,如果结果为负,说明前一个向量对应的点的极角更小,于是把它排在前面,很容易完成。如果两向量共线,则按距离由小到大排,代码如下:
list.sort((a, b) -> {
/* 按叉乘逆时针 */
int diff = cross(list.get(0), a, b);
if (diff == 0) {
/* 按距离由近到远 */
return (distance(list.get(0), a) - distance(list.get(0), b));
} else {
return -diff;
}
});
怎么利用叉乘的性质来判断删除哪些点呢?举如下例子:

初始点显然是 A 点,剩下的点按照上述算法描述的排序顺序标号,从 B 点开始不断加入凸包,如图:
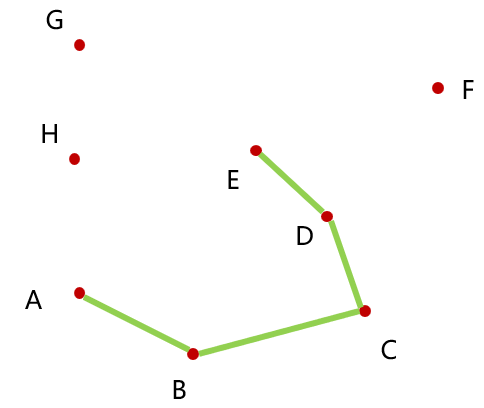
当加入 F 点后,我们要找前两个加入的点来做叉乘,如果

删除这一个点就够了吗?从图中看出,并不够。我们还要找凸包中 E 点之前的两个点 C 点和 D 点,

对于加入的每个点,都要与凸包中最近加入的两个点做叉乘运算,很显然,这里可以用栈结构来保存凸包中的点,代码如下:
Deque<Integer> stack = new ArrayDeque<Integer>();
stack.push(0);
stack.push(1);
int n = list.size();
for (int i = 2; i < n; i++) {
int top = stack.pop();
/* 如果当前元素与栈顶的两个元素构成的向量顺时针旋转或共线,则弹出栈顶元素 */
while (!stack.isEmpty() && cross(list.get(stack.peek()), list.get(top), list.get(i)) <= 0) {
top = stack.pop();
}
stack.push(top);
stack.push(i);
}
细节:距离判断
为什么对于共线的点,要按它们与初始点的距离从小到大排序呢?
考虑如下例子:

A、B、C、D 四点共线,算法会先加入 A、B 两点,当加入 C 时,

反之,如果不按距离由小到大排序,假如先加入 D 点,则下一步加入 C 点时,算法判断
完整代码
public static Set<Point> convexHull(Set<Point> points) {
if(points.size() <= 3) return points;
ArrayList<Point> list = new ArrayList<>(points);
int first = 0;
/* 找到最左下的点 */
for(int i = 0; i < list.size(); i++){
if(list.get(i).x() < list.get(first).x() || (list.get(i).x() == list.get(first).x() && list.get(i).y() < list.get(first).y()))
first = i;
}
swap(list, first, 0);
/* 按距离和极角排序 */
list.sort((a, b) -> {
int diff = cross(list.get(0), a, b);
if (diff == 0) {
return (distance(list.get(0), a) - distance(list.get(0), b));
} else {
return -diff;
}
});
Deque<Integer> stack = new ArrayDeque<Integer>();
/* 将前两个点压入栈中 */
stack.push(0);
stack.push(1);
int n = list.size();
for (int i = 2; i < n; i++) {
int top = stack.pop();
/* 如果当前元素与栈顶的两个元素构成的向量顺时针旋转或共线,则弹出栈顶元素 */
while (!stack.isEmpty() && cross(list.get(stack.peek()), list.get(top), list.get(i)) <= 0) {
top = stack.pop();
}
stack.push(top);
stack.push(i);
}
Set<Point> ans = new HashSet<>();
while(!stack.isEmpty()){
ans.add(list.get(stack.pop()));
}
return ans;
}
/* 叉乘 */
public static int cross(Point p, Point q, Point r) {
return (int)((q.x() - p.x()) * (r.y() - q.y()) - (q.y() - p.y()) * (r.x() - q.x()));
}
/* 求距离 */
public static int distance(Point p, Point q) {
return (int)((p.x()-q.x())*(p.x()-q.x())+(p.y()-q.y())*(p.y()- q.y()));
}
public static void swap(ArrayList<Point> list, int i, int j) {
Point temp = list.get(i);
list.set(i, list.get(j));
list.set(j, temp);
}
复杂度分析
时间复杂度为
最开始排序的部分:时间复杂度为
核心算法的部分:对于点集中的每一个点,都会入栈一次,在后面加点判断时,最多可能会出栈一次,时间复杂度为
故总的时间复杂度为
Andrew 算法
Andrew 算法是 Graham 算法的改进,改进的地方在排序部分。 Graham 算法据极角和距离来进行排序,可能引起较高的时间复杂度,而 Andrew 算法是先对 x 坐标由小到大进行排序,然后对于 x 坐标相等的点再按 y 坐标由小到大排序,对排序时的复杂度有所优化
那么按照什么顺序来更新点呢?Graham 算法的巧妙之处在于通过极角和距离,能让所有点按照逆时针顺序排好序,而 Andrew 算法中按坐标的排序做法就显得有些凌乱了
为了解决这个做法,只好把凸包的产生分为两部分。排序以后,最左下的点与最右上的点一定在凸包上,并且它们能把凸包分为上凸壳和下凸壳

那么对于下凸壳的部分,凸包的点按逆时针是以横坐标从小到大排列的;到达 H 点后,对于上凸壳的部分,凸包的点按逆时针又以横坐标从大到小排序
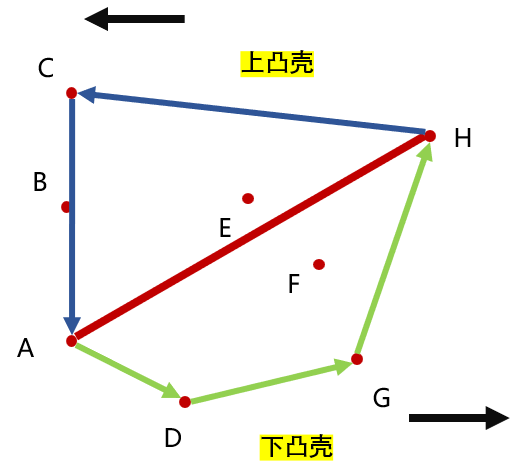
所以排完序后,我们要遍历更新两次,第一轮从正向遍历,得到下凸包部分;第二轮从逆向遍历,得到上凸包部分,更新的做法与 Graham 算法逻辑完全相同
实现细节
讲到这,可能还会有点疑惑,为什么一定要遍历两次呢?
举例:在第一轮从正向遍历的时候,先把 A、B 两点两点入栈,接下来遍历到 D 点,
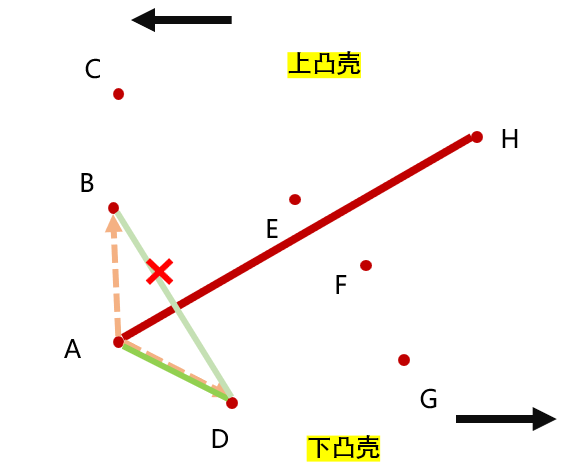
也就是说,按坐标这种特殊的排序方式,对于正向遍历一定只能得到下凸壳,逆向遍历一定只能得到上凸壳
完整代码
更新部分代码与 Graham 逻辑相同,只有两点特殊:
- 要分别正向、逆向遍历两次
- 设置一个哈希表,存放已经确定加入下凸壳部分的点,避免在逆向遍历时加入下凸壳的点,增加出栈操作
public static Set<Point> convexHull(Set<Point> points) {
if(points.size() <= 3) return points;
ArrayList<Point> list = new ArrayList<>(points);
list.sort((a, b) -> {
if((int)a.x()==(int)b.x()) return (int)(a.y() - b.y());
return (int)(a.x() - b.x());
});
Deque<Integer> stack = new ArrayDeque<Integer>();
Set<Integer> visited = new HashSet<>();
stack.push(0);
stack.push(1);
visited.add(0);
visited.add(1);
int n = list.size();
for (int i = 2; i < n; i++) {
int top = stack.pop();
visited.remove(top);
/* 如果当前元素与栈顶的两个元素构成的向量顺时针旋转或共线,则弹出栈顶元素 */
while (!stack.isEmpty() && cross(list.get(stack.peek()), list.get(top), list.get(i)) <= 0) {
top = stack.pop();
visited.remove(top);
}
stack.push(top);
visited.add(top);
stack.push(i);
visited.remove(i);
}
int m = stack.size();
for(int i = n-2; i >= 0; i--) {
if(!visited.contains(i)) {
int top = stack.pop();
visited.remove(top);
/* 如果当前元素与栈顶的两个元素构成的向量顺时针旋转或共线,则弹出栈顶元素 */
/* 不需要判断下凸壳的部分 */
while (stack.size() > m && cross(list.get(stack.peek()), list.get(top), list.get(i)) <= 0) {
top = stack.pop();
visited.remove(top);
}
stack.push(top);
visited.add(top);
stack.push(i);
visited.remove(i);
}
}
stack.pop();
Set<Point> ans = new HashSet<>();
while(!stack.isEmpty()){
ans.add(list.get(stack.pop()));
}
return ans;
}
复杂度分析
由于增加了哈希表,所以每个元素还是最多入栈出栈各一次,总时间复杂度仍为
因为这个算法优化了排序的性能,耗时往往比 Graham 要短