Word2vec 的基本思想是给每个单词初始化向量,使得其与出现在相似上下文中的单词向量相似。
算法:
- 对于文本中的每一个位置
,我们都有一个中心词 和上下文 - 根据
和 单词向量的相似性来计算给定 时上下文出现 的概率或给定 时上下文出现 的概率 - 由此计算词向量,使这个概率最大
损失函数推导
举如下图例,计算

对于语料库中的每个位置
那么我们就可以得到似然函数:
目标就是要求该函数取极值时
为了进行计算,我们需要对这个函数取对数,并加上负号来转化为求极小化问题,于是得到损失函数:
现在要解决的问题:如何表示
首先,对于每一个词
是中心词时,则向量为 是上下文时,则向量为
那么对于中心词
用两者向量的点积衡量它们的相似程度,点积越大则越相似。由于概率不能为负,所以将点积取幂,由于概率和要为 1,应归一化处理,于是就得到了如下概率表示:
其实也就是点积的 softmax 函数
假设每个向量有
首先初始化
求对
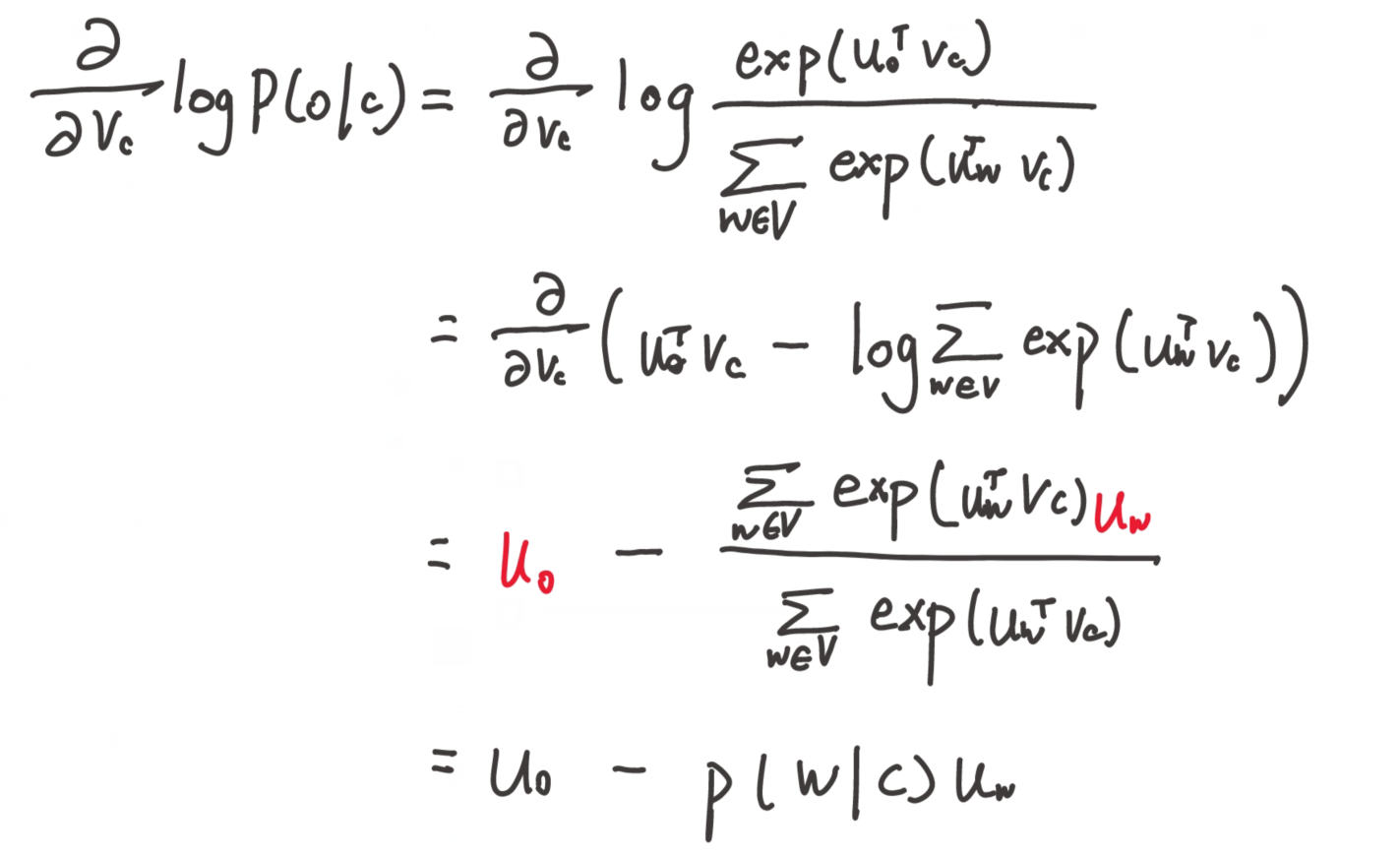
两种算法
- Continuous Bag of Words Model (CBOW),根据中心词周围的上下文来预测该词词向量
- Skip-Gram Model,与前者相反,根据中心词预测周围上下文的词的概率分布
CBOW 模型
首先,对于每一个词
是中心词时,则向量为 (输出向量) 是上下文时,则向量为 (输入向量)
设
模型步骤如下:
- 假设考虑窗口为 m,那么用每一个词的 one-hot 编码
,作为初始向量,那么对于 的上下文为: - 将输入词矩阵与每个词的 one-hot 向量做积,得
,输入词矩阵初始值可以随机取,由于 one-hot 编码是只有对应位置才为 1,所以得到的结果就是输入词矩阵对应词所在的列
CBOW 是要用上下文词预测中心词,接下来的问题是要把上下文词向量融合起来表示中心词向量,融合可有很多种办法,原论文中很朴素地采用直接相加,于是下一步是:
- 对上述向量求平均值
- 此时
就是计算出的中心词向量,而实际中心词向量为 ,所以将两者做点积 ,该值越大则说明两向量越相似,故该向量也成为分数向量 - 使用激活函数处理,将值转换为概率
- 我们希望生成的概率
与实际的 one-hot 比较,模型需不断学习矩阵 和 (因为这里的 one-hot 也可以看作概率,对应单词的概率为 1,其它为 0)
最后,每个单词的 one-hot 与输入词矩阵相乘就得到了词向量
结构如图:

那么如何学习
得损失函数为:
由于 y 为 one-hot 向量,其它部分均为 0,故公式可以写为:
当
从而优化目标函数公式为:
使用梯度下降法更新即可
Skip-Gram 模型
该模型与前者逻辑一样,只不过步骤刚好相反,前者是根据上下文向量求中心词概率并于 one-hot 比较,而该模型是根据中心词求上下文向量然后与 one-hot 向量比较
过程简要如下:
- 生成中心词的 one-hot 向量
- 用输入词矩阵乘,
- 生成分数向量
- 将分数向量转化为概率
- 比较
与 one-hot 向量
结构如图:

求目标函数时有些许差异,给定中心词时,假定输出的上下文的词间是独立的
同样使用梯度下降法更新
计算优化
让我们回到目标函数上。注意对
- 负采样 (Negative sampling),通过抽取负样本将问题转化为二分类问题
- Hierarchical softmax,通过构建哈夫曼树降低运算开销
Negative Sampling
不去遍历整个词汇表,而仅仅是抽取一些负样例做优化
考虑一对中心词和上下文词
现在考虑建立新的目标函数,如果两者确实来自语料库,就最大化概率
先令:
则:

取对小对数似然:
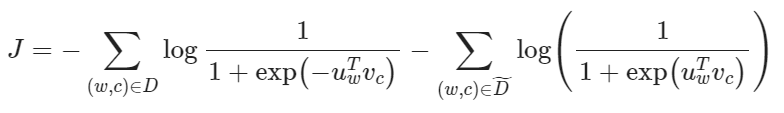
负样本按如下分布抽取:
四分之三是信息检索领域里的一个经典参数,这个参数只是因为实际效果好而试出来的,比如如下计算:
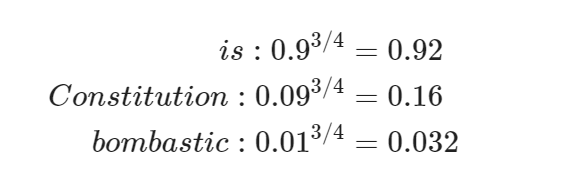
低频词 "Bombastic" 现在被抽样的概率是之前的三倍,而 "is" 只提高了一点点,它能够较大提升低频词的抽取概率
Hierarchical Softmax
Hierarchical softmax 使用一个哈夫曼树来降低训练的成本。树中的每个叶节点都是一个单词。每个叶节点到根节点的路径是唯一确定的,我们考虑不直接优化单词的向量,而是优化所有非叶节点的向量,那么代价就能从原来的
具体计算如下:
- 设
为从根节点到叶节点 的路径中节点数目 - 设
为到叶节点 的第 个节点,如 为根节点, - 对每个内部节点,定义它的左子节点(右子节点也可以)为
- [[x]] 的含义是:如果 x 为真,则值为 -1,否则值为 1

则 Hierarchical softmax 可定义为:
详细解释:
表示如果 的左子节点为到 的路径,则值为 1,否则为 -1 计算的即为向量与每个非叶向量的相似度
也就是说,非叶节点的向量起到一个“导航”的作用,我们要优化它们使得最终能“走到”概率最大的叶节点。
虽然这种方法在后面的工作就不再使用了,但思想非常巧妙,值得学习,也是面试高频考察点。