Note07-B+ 树索引详解
这是一种以树型结构来组织索引项的多级索引。非叶结点指针指向索引块,叶结点指针指向主文件的数据块或数据记录,叶结点的最后一个指针始终指向下一个叶结点。
B+ 树查找、插入、删除等操作,见文章:B+树看这一篇就够了(B+树查找、插入、删除全上)
:::caution 注意
接下来的内容均从此文复制而来,如有侵权,请联系我
:::
插入操作
在 B+ 树中插入关键字时,需要注意以下几点:
- 插入的操作全部都在叶子结点上进行,且不能破坏关键字自小而大的顺序;
- 由于 B+ 树中各结点中存储的关键字的个数有明确的范围,做插入操作可能会出现结点中关键字个数超过阶数的情况,此时需要将该结点进行 “分裂”;
我们依旧以之前介绍查找操作时使用的图对插入操作进行说明,需要注意的是,B+ 树的阶数 M = 3 ,且 ⌈M/2⌉ = 2(取上限) 、⌊M/2⌋ = 1(取下限) :

B+ 树中做插入关键字的操作,有以下 3 种情况:
1、 若被插入关键字所在的结点,其含有关键字数目小于阶数 M,则直接插入;
比如插入关键字 12 ,插入关键字所在的结点的 [10,15] 包含两个关键字,小于 M ,则直接插入关键字 12 。

2、 若被插入关键字所在的结点,其含有关键字数目等于阶数 M,则需要将该结点分裂为两个结点,一个结点包含 ⌊M/2⌋ ,另一个结点包含 ⌈M/2⌉ 。同时,将 ⌈M/2⌉ 的关键字上移至其双亲结点。假设其双亲结点中包含的关键字个数小于 M,则插入操作完成。
插入关键字 95 ,插入关键字所在结点 [85、91、97] 包含 3 个关键字,等于阶数 M ,则将 [85、91、97] 分裂为两个结点 [85、91] 和结点 [97] , 关键字 95 插入到结点 [95、97] 中,并将关键字 91 上移至其双亲结点中,发现其双亲结点 [72、97] 中包含的关键字的个数 2 小于阶数 M ,插入操作完成。

3、在第 2 情况中,如果上移操作导致其双亲结点中关键字个数大于 M,则应继续分裂其双亲结点。
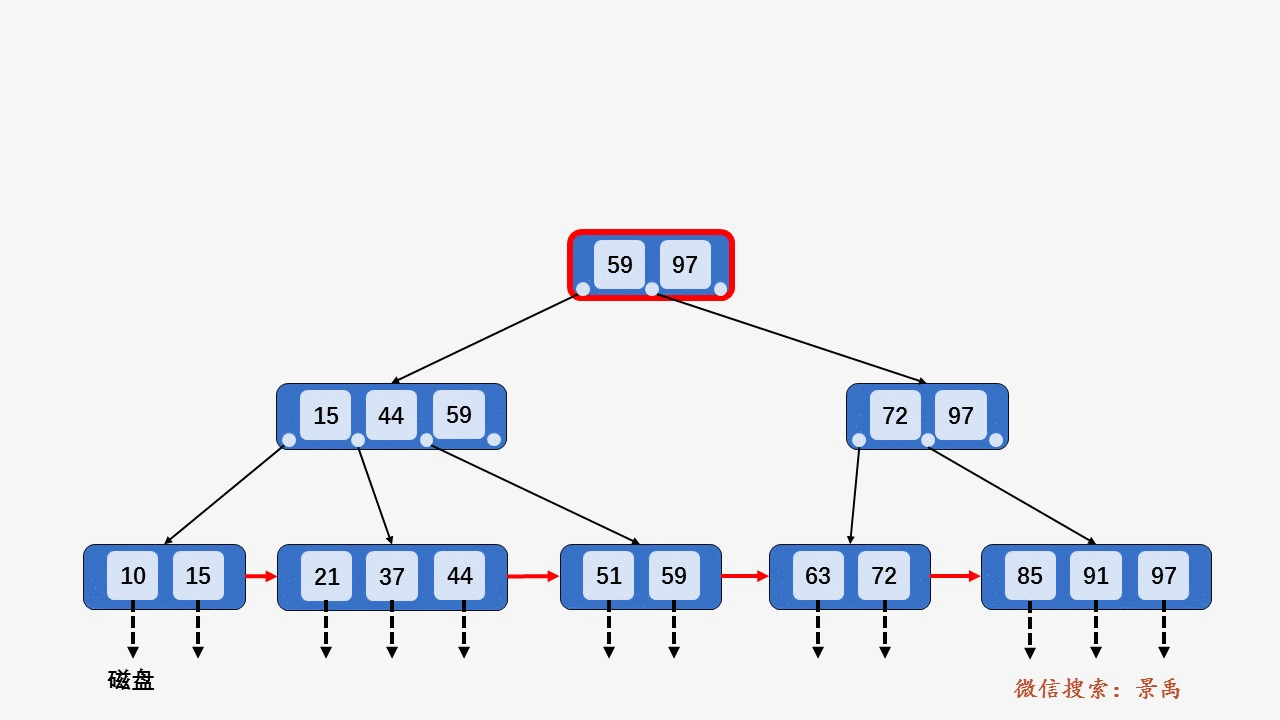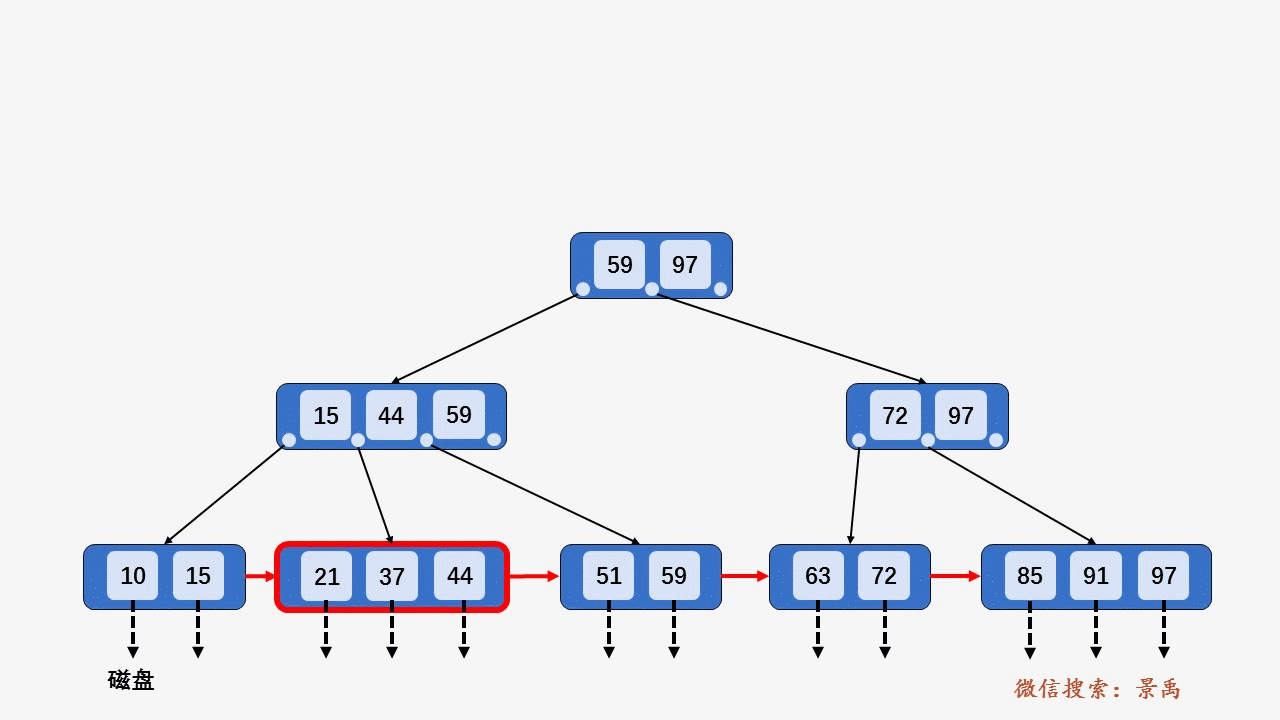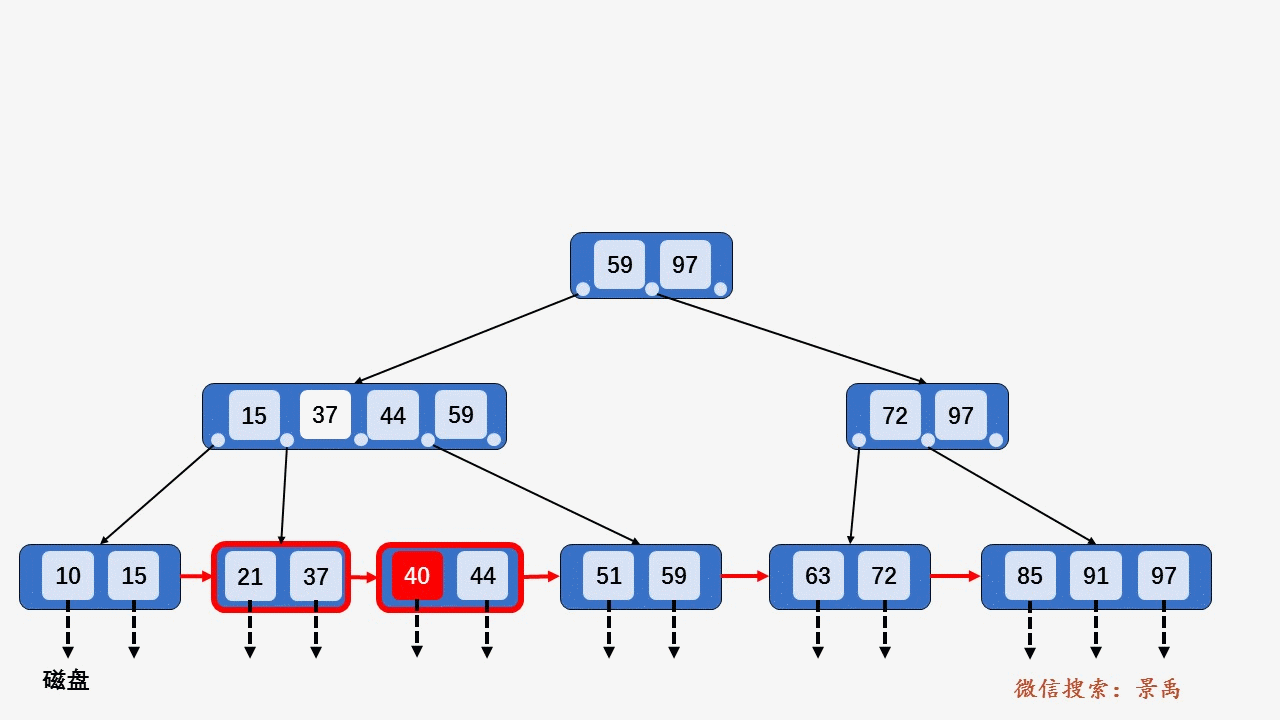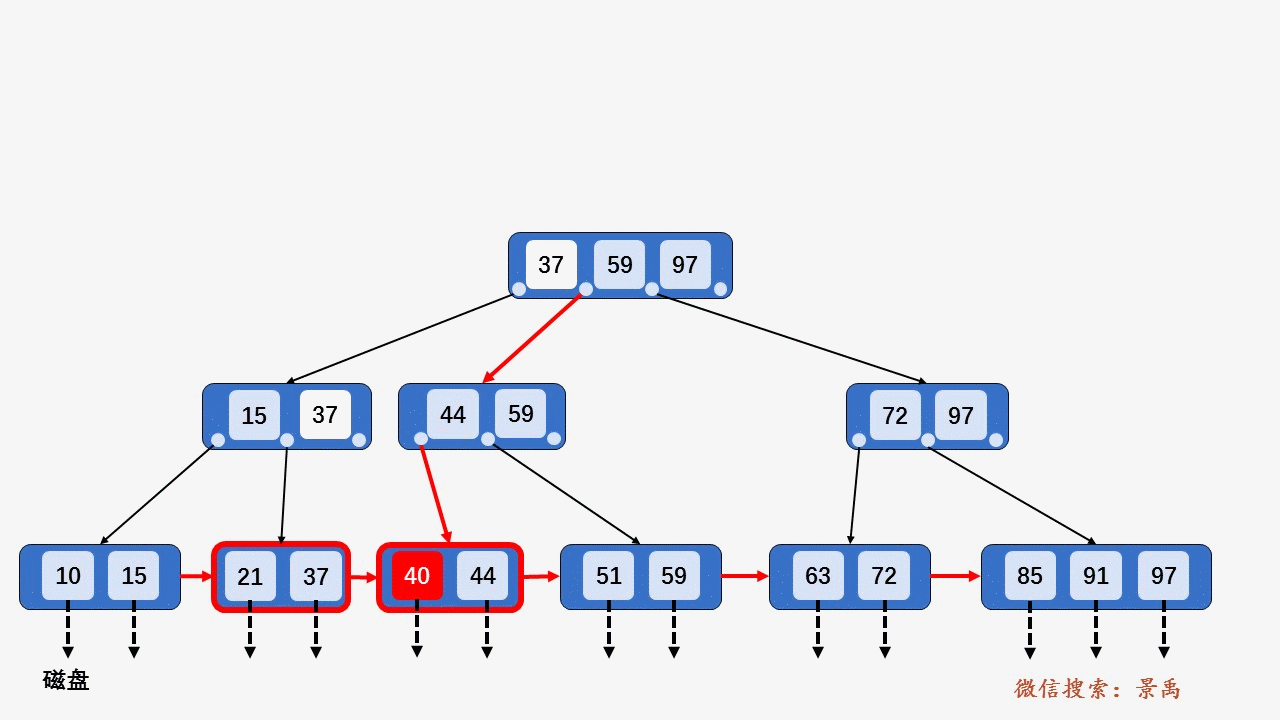
插入关键字 40 ,按照第 2 种情况将结点分裂,并将关键字 37 上移到父结点,发现父结点 [15、37、44、59] 包含的关键字的个数大于 M ,所以将结点 [15、37、44、59] 分裂为两个结点 [15、37] 和结点 [44、59] ,并将关键字 37 上移到父结点中 [37、59、97] . 父结点包含关键字个数没有超过 M ,插入结束。
4、若插入的关键字比当前结点中的最大值还大,破坏了 B+ 树中从根结点到当前结点的所有索引值,此时需要及时修正后,再做其他操作。
插入关键字 100,由于其值比最大值 97 还大,插入之后,从根结点到该结点经过的所有结点中的所有值都要由 97 改为 100。改完之后再做分裂操作。

删除操作
在 B+ 树中删除关键字时,有以下几种情况:
1、 找到存储有该关键字所在的结点时,由于该结点中关键字个数大于 ⌈M/2⌉,做删除操作不会破坏 B+ 树,则可以直接删除。
删除关键字 91,包含关键字 91 的结点 [85、91、97] 中关键字的个数 3 大于 ⌈M/2⌉ = 2 ,做删除操作不会破坏 B+ 树的特性,直接删除。

2、 当删除某结点中最大或者最小的关键字,就会涉及到更改其双亲结点一直到根结点中所有索引值的更改。
以删除整颗 B+ 树中最大的关键字 97 为例,查找并删除关键字 97 , 然后向上回溯,将所有关键字 97 替换为次最大的关键字 91 :

3、 当删除该关键字,导致当前结点中关键字个数小于 ⌈M/2⌉,若其兄弟结点中含有多余的关键字,可以从兄弟结点中借关键字完成删除操作。
当删除某个关键字之后,结点中关键字个数小于 ⌈M/2⌉ ,则不符合 B+ 树的特性,则需要按照 3 和 4 两种情况分别处理。以删除关键字 51 为例,由于其兄弟结点 [21、37、44] 中含有 3 个关键字,所以可以选择借一个关键字 44,同时将双亲结点中的索引值 44 修改 37 ,删除过程如下图所示:

4、 第 3 种情况中,如果其兄弟结点没有多余的关键字,则需要同其兄弟结点进行合并。
为了说明这种情况,我们在第 3 种情况最终得到的 B+ 树之上进行删除操作。第 3 种情况删除关键字 51 之后得到如下所示 B+ 树:
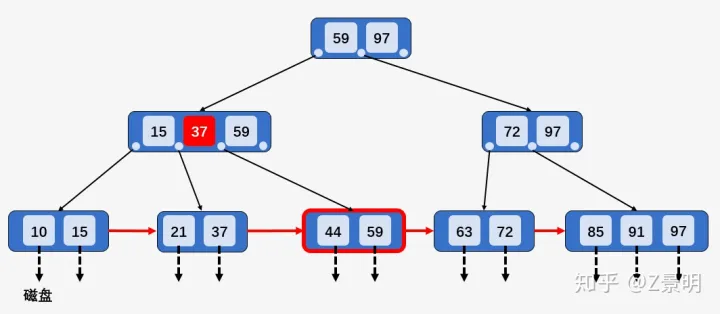
我们以删除上面这个 B+ 树中的关键字 59 说明第 4 种情况,首先查找到关键 59 所在结点 [44、59] ,发现该结点的兄弟结点 [21、37] 包含的关键字的个数 2 等于 ⌈M/2⌉, 所以删除关键字 59 ,并将结点 [21、37] 和 [44] 进行合并 [21、37、44] ,然后向上回溯,将所有关键字 59 替换为次最大的关键字 44 :

5、 当进行合并时,可能会产生因合并使其双亲结点破坏 B+ 树的结构,需要依照以上规律处理其双亲结点。
删除关键字 63,当删除关键字后,该结点中只剩关键字 72,且其兄弟结点 [85、91] 中只有 2 个关键字,所以将 [72] 和 [85、91] 进行合并,向上回溯,删除结点 [72、91] 当中的关键字 72 ,此时结点中只有关键 91 ,不满足 B+ 树中结点关键字个数要求,但其兄弟结点 [15、44、59] 中包含的 3 个关键字,所以从其兄弟结点当中借一个关键字 59 , 再对其兄弟结点的父结点中的关键字进行调整,将关键字 59 替换为 44 .

总之,在 B+ 树中做删除关键字的操作,采取如下的步骤:
- 删除该关键字,如果不破坏 B+ 树本身的性质,直接完成删除操作(情况 1);
- 如果删除操作导致其该结点中最大(或最小)值改变,则应相应改动其父结点中的索引值(情况 2);
- 在删除关键字后,如果导致其结点中关键字个数不足,有两种方法:一种是向兄弟结点去借,另外一种是同兄弟结点合并(情况 3、4 和 5)。(注意这两种方式有时需要更改其父结点中的索引值。)
感谢此文作者!写得太好了!