Note09- 查询优化

设有如下两个关系：

• $S(S\mathrm{\#},SN)$
• $SC(S\mathrm{\#},C\mathrm{\#})$

有如下 SQL 语句：

SELECT DISTINCT S.SN
FROM S,SC
WHERE S.S#=SC.S# AND SC.C#='C2'

我们可以将它转换为多种等价的关系代数表达式，且执行效率很可能有较大差别

• $Q_1={\mathrm{\Pi }}_{SN}({\sigma }_{(S.S\mathrm{\#}=SC.S\mathrm{\#})\wedge (SC.C\mathrm{\#}{=}^{\prime }C{2}^{\prime })}(S\times SC))$
  • 计算 $S$ 和 $SC$ 的笛卡尔积
  • 按照选择条件，选择满足要求的元组
  • 投影输出
• $Q_2={\mathrm{\Pi }}_{SN}({\sigma }_{SC.C\mathrm{\#}{=}^{\prime }C{2}^{\prime }}(S{\bowtie }_{S.S\mathrm{\#}=SC.S\mathrm{\#}}SC))$
  • 计算自然连接
  • 读取中间文件快
  • 投影输出
• $Q_3={\mathrm{\Pi }}_{SN}(({\sigma }_{SC.C\mathrm{\#}{=}^{\prime }C{2}^{\prime }}SC){\bowtie }_{S.S\mathrm{\#}=SC.S\mathrm{\#}}S)$
  • 对 $SC$ 作选择运算
  • 读取 $S$ 表，把读入的 $S$ 元组和内存中的 $SC$ 元组作连接
  • 投影输出

关系代数等价转换规则

• 选择串接律。
  • ${\sigma }_{c1AND\cdots ANDcn}\equiv {\sigma }_{c1}({\sigma }_{c2}(\cdots ({\sigma }_{cn}(E))\cdots ))$
• 选择交换律。
  • ${\sigma }_{c1}({\sigma }_{c2}(E))\equiv {\sigma }_{c2}({\sigma }_{c1}(E))$
• 投影串接律。
  • ${\mathrm{\Pi }}_{L1}({\mathrm{\Pi }}_{L2}(\cdots ({\mathrm{\Pi }}_{Ln}(E))\cdots ))\equiv {\mathrm{\Pi }}_{L1}(E)$，其中，$L1\subseteq L1\subseteq \cdots \subseteq Ln$
• 选择投影交换律。
  • ${\mathrm{\Pi }}_L({\sigma }_C(E))\equiv {\sigma }_C({\mathrm{\Pi }}_L(E))$，假定 $C$ 只涉及 $L$ 中的属性
• 连接和笛卡尔乘积的交换律。
  • $E_1\times E_2\equiv E_2\times E_1,E_1{\bowtie }_C{E}_2\equiv E_2{\bowtie }_C{E}_1$
• 集合操作的交换律。
  • $E_1\cup E_2\equiv E_2\cup E_1$
• 连接、笛卡尔乘积和集合操作的结合律
• 选择、连接和笛卡尔乘积的分配律。
• 投影、连接和笛卡尔乘积的分配律。
  • ${\mathrm{\Pi }}_L(E_1{\bowtie }_C{E}_2)\equiv ({\mathrm{\Pi }}_{L1}(E_1){\bowtie }_C{\mathrm{\Pi }}_{L2}(E_2))$
• 选择与集合操作的分配律
• 投影与集合操作的分配律

表达式结果大小的估计

定义如下符号：

• $n_r$：关系 $r$ 的元组数
• $b_r$：包含关系 $r$ 中元组的磁盘块数
• $l_r$：关系 $r$ 中每个元组的字节数
• $f_r$：关系 $r$ 的块因子，一个磁盘块能容纳 $r$ 中元组的个数
• $V(A,r)$：关系 $r$ 中属性 $A$ 中出现的非重复值的个数

当 $r$ 中 $A$ 属性上的取值分布是均匀的，运算结果大小的估计如下：

• 投影 ${\mathrm{\Pi }}_A(r)$

  • 估计值为 $V(A,r)$

• 选择 ${\sigma }_{A=a}(r)$

  • 估计值为 $n_r/V(A,r)$

• 选择 ${\sigma }_{A\le v}(r)$

  • 如果 $v<min(A,r)$，则估计值为 0
  • 如果 $v\ge max(A,r)$，则估计值为 $n_r$
  • 否则，估计值为 $\frac{v-min(A,r)}{max(A,r)-min(A,r)}\times n_r$

• 合取 ${\sigma }_{{\theta }_1\wedge {\theta }_2\wedge \cdots \wedge {\theta }_k}(r)$

  • 对于每个 ${\theta }_i$，估计选择大小为 $s_i$，则为 $n_r\times \frac{s_1\times s_2\times \cdots \times s_k}{n_r^k}$

• 析取 ${\sigma }_{{\theta }_1\vee {\theta }_2\vee \cdots \vee {\theta }_k}(r)$

  • $(1-(1-\frac{s_1}{n_r})\times (1-\frac{s_2}{n_r})\times \cdots \times (1-\frac{s_k}{n_r}))\times n_r$

• 取反 ${\sigma }_{\mathrm{\neg }\theta }(r)$

  • 在无空值的情况下，估计值为 $n_r-s_{\theta }$
  • 在有空值得请开给你下，估计值为 $n_r-n_{null}-s_{\theta }$

• 笛卡尔积 $r\times s$

  • 元组个数 $n_r\times n_s$，每个元组占 $l_r+l_s$ 个字节

• 自然连接 $r(R)$ 和 $s(S)$

  • 若 $R\cap S$ 为空，则类似于笛卡尔积的结果
  • 若 $R\cap S$ 为 $R$ 的码，则可知 $s$ 的一个元组至多与 $r$ 的一个元组相连接，因此自然连接结果的元组数小于等于 $n_s$，若 $R\cap S$ 构成 $S$ 中参照 $R$ 的外码，则自然连接结果等于 $n_s$，反之亦然
  • 若 $R\cap S$ 既不是 $R$ 的码也不是 $S$ 的码，则 $min(n_r\times \frac{n_s}{V(A,s)},n_s\times \frac{n_r}{V(A,r)})$

• 聚集

  • $V(A,r)$

• 集合运算

  • 和合取、析取、取反的估计方法一样

• 外连接（结果上界）

  • $r$ 左外连接 $s$：$r$ 与 $s$ 自然连接的大小估计值 $+n_r$
  • $r$ 右外连接 $s$：$r$ 与 $s$ 自然连接的大小估计值 $+n_s$
  • $R$ 全外连接 $s$：$r$ 与 $s$ 自然连接的大小估计值 $+n_s+n_r$

启发式关系代数优化算法

• 规则 1：选择和投影操作尽早执行
• 规则 2：把某些选择操作与笛卡尔乘积相结合，形成一个连接操作
• 规则 3：同时执行相同关系上的多个选择和投影操作
• 规则 4：把投影操作与连接操作结合起来执行
• 规则 5：提取公共表达式

具体算法如下：

• 把形如 ${\sigma }_{F1\wedge F2\wedge \cdots \wedge Fn}(E)$ 的选择表达式变成串接形式 ${\sigma }_{F1}({\sigma }_{F2}(\cdots ({\sigma }_{Fn}(E))))$
• 对每个选择，依据定理 L4 至 L9 尽可能把它移至树的底部
• 对每个投影，依据定理 L3，L7，L10 和 L5，尽可能把它移至树的底部
• 依据定理 L4 至 L5 把串接的选择和投影组合为单个选择、单个投影，或者一选择后跟一个投影
• 对修改后的语法树，将其内结点按以下方式分组：
  • 每个二元运算结点（积、并、差、连接等）和其所有一元运算直接祖先结点放在一组
  • 对于其后代结点，若后代结点是一串一元运算且以树叶为终点，则将这些一元运算结点放在该组中
  • 若该二元运算结点是笛卡儿积，且其后代结点不能和它组合成等连接，则不能将后代结点归入该组
• 产生一个程序：它以每组结点为一步，但后代组先执行。

举例

查询：查出 1978 年 1 月 1 日前被借出的所有书的书名

SELECT Title FROM XLOANS WHERE Data <= 1/1/78

XLOANS 视图为

CREATE VIEW XLOANS as SELECT * 
FROM LOANS, BORROWERS,
WHERE BORROWERS.CARD_NO=LOANS.CARD_NO AND BOOKS.LC_NO=LOANS.LC_NO

转换成关系代数表达式：${\mathrm{\Pi }}_{TITLE}({\sigma }_{Data<{=}^{\prime }1/1/{78}^{\prime }}(XLOANS))$

首先，我们要将选择表达式变成串接的形式，然后对于每个选择，尽可能把它移至树的底部

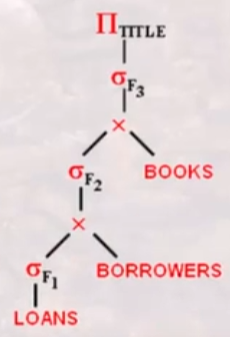
对每个投影，尽可能移动到底部，由 ${\mathrm{\Pi }}_{TITLE}={\mathrm{\Pi }}_{TITLE}({\mathrm{\Pi }}_{TITLE,BOOKS.LC\mathrm{\_}NO,LOANS.LC\mathrm{\_}NO})$

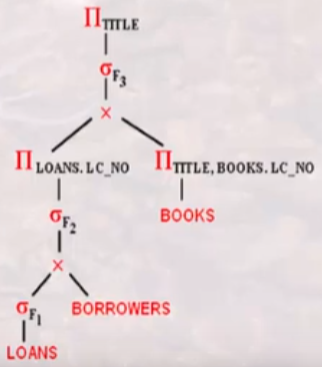
类似处理 BORRWERS 和 LOANS 的投影：

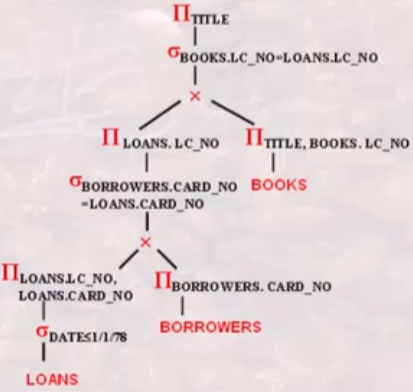
然后分组：