壹 - 实现计算图与自动求导

在前一篇文章中，我们搭建过一个简单的两层神经网络：

z = W_{2}^{T} ReLU (W_{1}^{T} x)

在这个神经网络中，我们通过手动计算梯度再用随机梯度下降法实现了对两个权重矩阵的更新。但是一旦层数变多，模型变得更加复杂，手动计算就非常烦琐了。本文将搭建深度学习框架中最重要的结构——计算图，并由此实现自动求导机制。

计算图原理

计算图就是一个表示运算的有向无环图。图中的每个节点都表示一个变量和一种运算（叶子节点只表示变量）。比如下面这个计算：

y = f (x_{1}, x_{2}) = l n (x_{1}) + x_{1} x_{2} - s i n x_{2}

可以构造计算图：

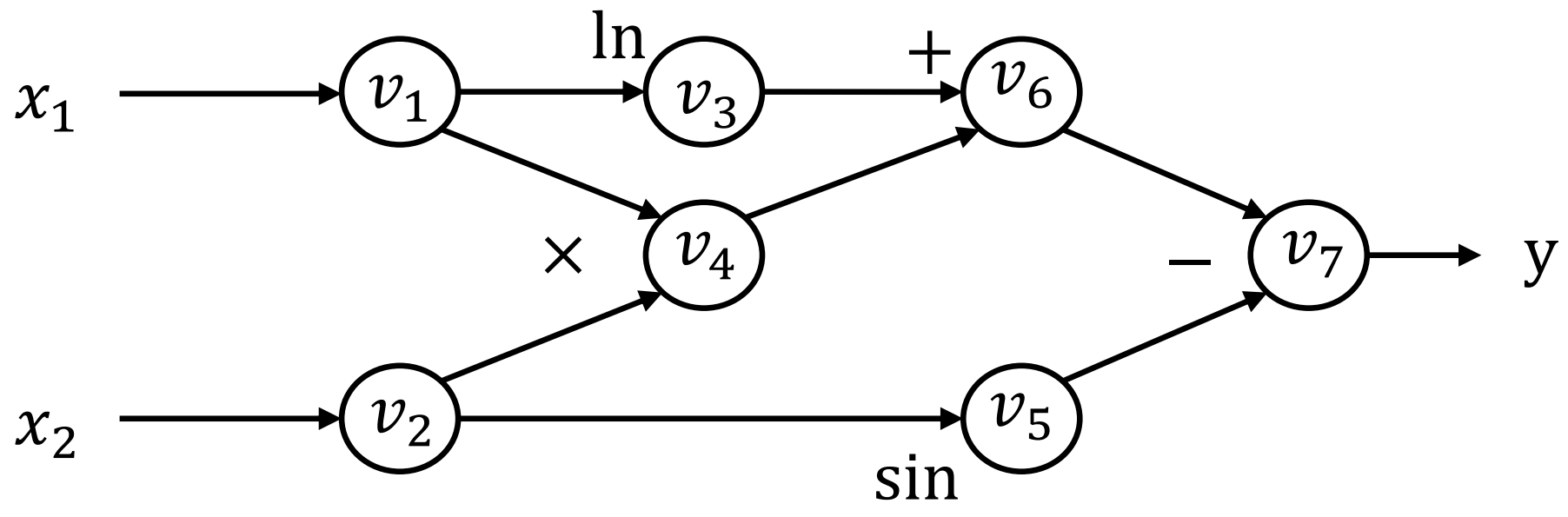
vb34n

正向计算求值的过程我们称为正向传播

\begin{aligned} v_{1} = x_{1} = 2 \\ v_{2} = x_{2} = 5 \\ v_{3} = \ln v_{1} = \ln 2 = 0.693 \\ v_{4} = v_{1} \times v_{2} = 10 \\ v_{5} = \sin v_{2} = \sin 5 = - 0.959 \\ v_{6} = v_{3} + v_{4} = 10.693 \\ v_{7} = v_{6} - v_{5} = 10.693 + 0.959 = 11.652 \\ y = v_{7} = 11.652 \end{aligned}

那么如何求得结果 $y$ 对中间某个值的导数呢，我们也可以从两个方向来做

正向模式

一种很自然的想法是从图中的叶子节点开始，按拓扑排序的顺序计算每个中间节点对原始输入的倒数，记 $\dot{v_{i}} = \frac{\partial v_{i}}{\partial x_{1}}$ ，则：

\begin{aligned} {\dot{v}}_{1} = 1 \\ {\dot{v}}_{2} = 0 \\ {\dot{v}}_{3} = {\dot{v}}_{1} / v_{1} = 0.5 \\ {\dot{v}}_{4} = {\dot{v}}_{1} v_{2} + {\dot{v}}_{2} v_{1} = 1 \times 5 + 0 \times 2 = 5 \\ {\dot{v}}_{5} = {\dot{v}}_{2} \cos v_{2} = 0 \times \cos 5 = 0 \\ {\dot{v}}_{6} = {\dot{v}}_{3} + {\dot{v}}_{4} = 0.5 + 5 = 5.5 \\ {\dot{v}}_{7} = {\dot{v}}_{6} - {\dot{v}}_{5} = 5.5 - 0 = 5.5 \end{aligned}

这种做法看起来很简单，但是它有一个缺陷在于，对于函数 $f : R^{n} \to R^{k}$ ，当 $n$ 比较小时，它的运算量很小，但是深度学习的场景下，往往输出数量 $k$ 很小（仅仅是一个向量甚至只是一个标量），但是输入的参数数量 $n$ 却非常庞大，使用这种方法的计算代价会非常大。

反向模式

顾名思义，这种做法就是从输出节点逆着求导，记 $v_{i}$ 的伴随值 $\overset{―}{v_{i}} = \frac{\partial y}{\partial v_{i}}$ ，则按逆向拓扑排序序列计算：

\begin{aligned} \overset{―}{v_{7}} = \frac{\partial y}{\partial v_{7}} = 1 \\ \overset{―}{v_{6}} = \overset{―}{v_{7}} \frac{\partial v_{7}}{\partial v_{6}} = \overset{―}{v_{7}} \times 1 = 1 \\ \overset{―}{v_{5}} = \overset{―}{v_{7}} \frac{\partial v_{7}}{\partial v_{5}} = \overset{―}{v_{7}} \times (- 1) = - 1 \\ \overset{―}{v_{4}} = \overset{―}{v_{6}} \frac{\partial v_{6}}{\partial v_{4}} = \overset{―}{v_{6}} \times 1 = 1 \\ \overset{―}{v_{3}} = \overset{―}{v_{6}} \frac{\partial v_{6}}{\partial v_{3}} = \overset{―}{v_{6}} \times 1 = 1 \\ \overset{―}{v_{2}} = \overset{―}{v_{5}} \frac{\partial v_{5}}{\partial v_{2}} + \overset{―}{v_{4}} \frac{\partial v_{4}}{\partial v_{2}} = \overset{―}{v_{5}} \times \cos v_{2} + \overset{―}{v_{4}} \times v_{1} = - 0.284 + 2 = 1.716 \\ \overset{―}{v_{1}} = \overset{―}{v_{4}} \frac{\partial v_{4}}{\partial v_{1}} + \overset{―}{v_{3}} \frac{\partial v_{3}}{\partial v_{1}} = \overset{―}{v_{4}} \times v_{2} + \overset{―}{v_{3}} \frac{1}{v_{1}} = 5 + \frac{1}{2} = 5.5 \end{aligned}

注意一个节点被多个节点作为输入节点的情况：

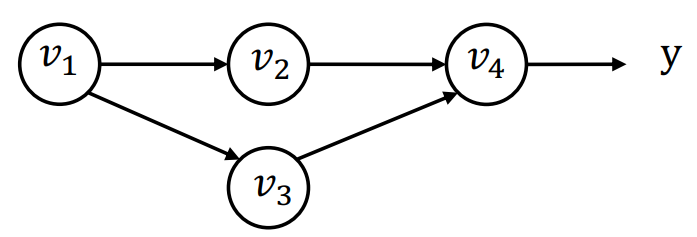
7655y

当计算得到 $\overset{―}{v_{2}}$ 和 $\overset{―}{v_{3}}$ 后，怎么计算 $\overset{―}{v_{1}}$ 呢？此时可以把 $y$ 看作关于 $v_{2}$ 和 $v_{3}$ 的二元函数： $y = f (v_{2}, v_{3})$ ，则：

\overset{―}{v_{1}} = \frac{\partial y}{\partial v_{1}} = \frac{\partial f (v_{2}, v_{3})}{\partial v_{2}} \frac{\partial v_{2}}{\partial v_{1}} + \frac{\partial f (v_{2}, v_{3})}{\partial v_{3}} \frac{\partial v_{3}}{\partial v_{1}} = \overset{―}{v_{2}} \frac{\partial v_{2}}{\partial v_{1}} + \overset{―}{v_{3}} \frac{\partial v_{3}}{\partial v_{1}}

因此，我们可以定义局部伴随值，对于每个把 $v_{i}$ 作为输入的节点， $\overset{―}{v_{i \to j}} = {\bar{v}}_{j} \frac{\partial v_{j}}{\partial v_{i}}$ ，则：

\overset{―}{v_{i}} = \sum_{j \in next (i)} \overset{―}{v_{i \to j}}

自动求导

到此，我们就能给出反向模式的自动求导算法：

2mi9g

在具体实现时，对于每一个节点的伴随值和局部伴随值我们也作为一个计算图节点来表达。举如下计算图的例子：

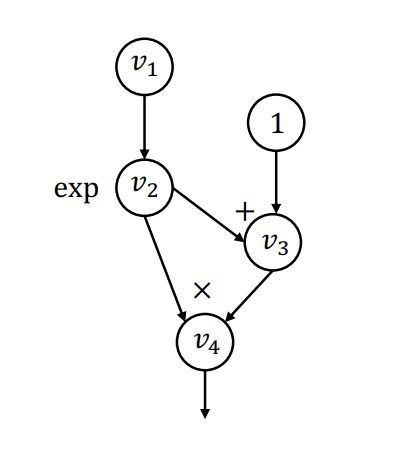
nl7jx

则算法流程如下：

初始化 $v_{4}$ 的伴随值为 1。因此，第一步计算得到 ${\overset{―}{v}}_{i} = 1$

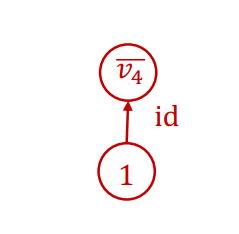
t3hvq

对于 $v_{4}$ 的输入 $v_{2}$ ，计算 $\overset{―}{v_{2 \to 4}} = \overset{―}{v_{4}} \times v_{3}$ ，这一步计算也能用计算图来表示。将这一步计算得到局部的伴随值加入词典中，对于 $v_{3}$ ，它只有一个输出，所以可以直接计算得到

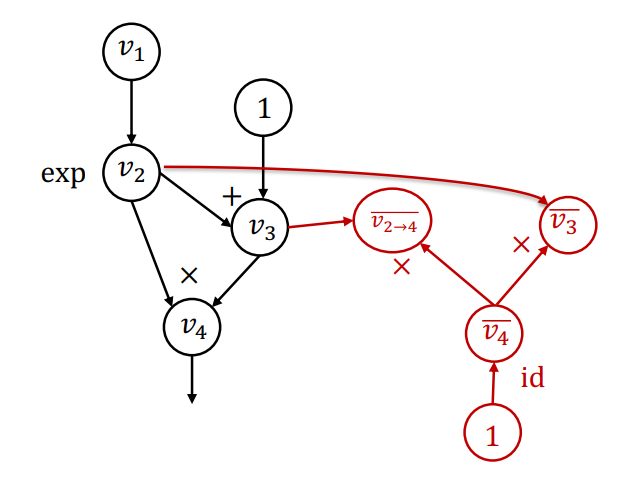
evrpn

最终，算法得到的扩展计算图为

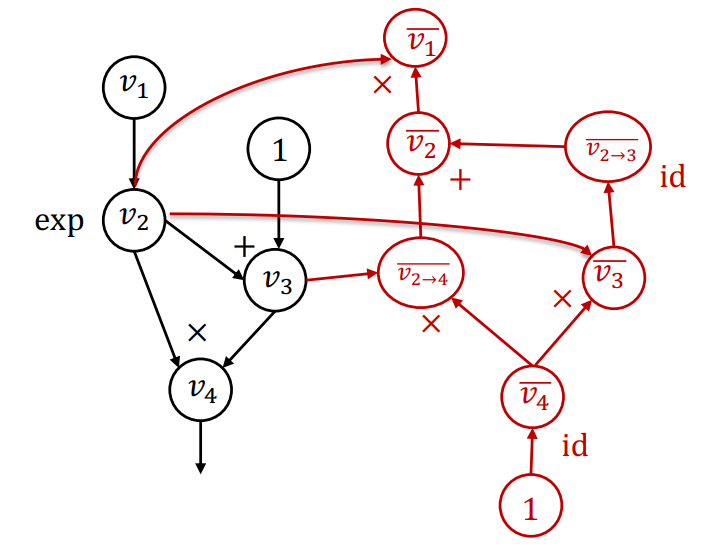
6we9z

这种反向模式的算法与通常意义上的反向传播似乎并不相同，为什么要这样扩展计算图来计算，而不是直接将梯度计算并保存到每个原始的计算图节点中呢？

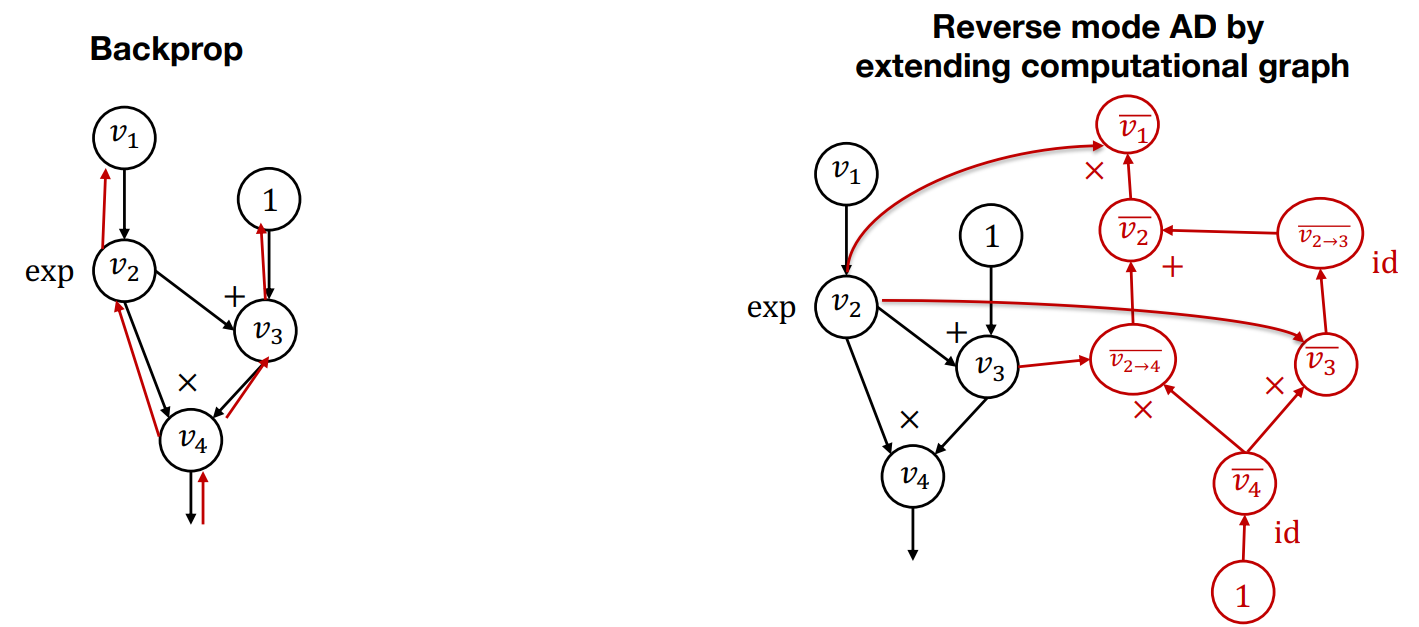
17s7k

在反向传播中，我们的伴随值都丢失了，无法计算梯度的梯度
在反向模式中，我们可以进一步扩展计算图得到我们想要的结果，并且在计算过程中可以做进一步的优化

因此，第一代的框架（caffe, cuda-convnet）等都用的是反向传播，而现代的框架（PyTorch, TensorFlow）等都是用反向模式进行自动求导。

Jacobian 矩阵

我们上述的做法都是基于标量的，如何扩展到多维向量呢？可以用 Jacobian 矩阵解决这个问题：

设 $f : R^{m \times n} \to R$ ， $y = f (Z)$ ，则

\bar{Z} = [\begin{array}{ccc} \frac{\partial y}{\partial Z_{1, 1}} & \dots & \frac{\partial y}{\partial Z_{1, n}} \\ \dots & \dots & \dots \\ \frac{\partial y}{\partial Z_{m, 1}} & \dots & \frac{\partial y}{\partial Z_{m, n}} \end{array}]

代码实现

接下来就开始实现计算图以及反向模式自动求导吧！这部分内容也对应于 CMUDeep Learning Systems 课程的作业 1

计算图节点抽象

由前文说到的，每一个计算图节点都要保存一个变量和一个运算，定义我们的计算图节点 Value 类：

class Value:
    """A value in the computational graph."""
    # trace of computational graph
    op: Optional[Op]
    inputs: List["Value"]
    # The following fields are cached fields for
    # dynamic computation
    cached_data: NDArray
    requires_grad: bool
    def realize_cached_data(self): # 得到节点对应的变量
    def is_leaf(self): # 是否为叶节点
    def __del__(self):
    def _init(self,op: Optional[Op],inputs: List["Tensor"],*,num_outputs: int = 1,cached_data: List[object] = None,requires_grad: Optional[bool] = None):
    @classmethod
    def make_const(cls, data, *, requires_grad=False): # 建立一个用data生成的独立的节点
    def make_from_op(cls, op: Op, inputs: List["Value"]):# 根据op生成节点

op：表示这个节点的运算操作
inputs：是一个列表，保存所有前向计算图节点
cached_data：实际上就是保存这个节点的变量
require_grad：该节点是否需要进行梯度计算

函数 realize_cached_data 的具体实现：

def realize_cached_data(self):
        """Run compute to realize the cached data"""
        # avoid recomputation
        if self.cached_data is not None:
            return self.cached_data
        # note: data implicitly calls realized cached data
        self.cached_data = self.op.compute(
            *[x.realize_cached_data() for x in self.inputs]
        )
        self.cached_data
        return self.cached_data

这个函数是最关键的函数，它通过委托 op 类下的 compute 函数对输入节点进行计算求值

运算操作抽象

op 类主要就是定义两个操作：

正向计算
反向求导 ${\bar{v}}_{j} \frac{\partial v_{j}}{\partial v_{i}}$

class Op:
    """Operator definition."""
    def compute(self, *args: Tuple[NDArray]):
        """Calculate forward pass of operator.

        Parameters
        ----------
        input: np.ndarray
            A list of input arrays to the function

        Returns
        -------
        output: nd.array
            Array output of the operation

        """

    def gradient(
        self, out_grad: "Value", node: "Value"
    ) -> Union["Value", Tuple["Value"]]:
        """Compute partial adjoint for each input value for a given output adjoint.

        Parameters
        ----------
        out_grad: Value
            The adjoint wrt to the output value.

        node: Value
            The value node of forward evaluation.

        Returns
        -------
        input_grads: Value or Tuple[Value]
            A list containing partial gradient adjoints to be propagated to
            each of the input node.
        """
	
    def gradient_as_tuple(self, out_grad: "Value", node: "Value") -> Tuple["Value"]:
        """ Convenience method to always return a tuple from gradient call"""

Tensor 类的实现

前面提到，每一个 Tensor 都是一个计算图节点，因此，其是 Value 类的一个子类。

class Tensor(Value):
    grad: "Tensor"
    def __init__(self,array,*,device: Optional[Device] = None,dtype=None,requires_grad=True,**kwargs):
    @staticmethod
    def _array_from_numpy(numpy_array, device, dtype):
    @staticmethod
    def make_from_op(op: Op, inputs: List["Value"]):
    @staticmethod
    def make_const(data, requires_grad=False):
    @property
    def data(self):
    @data.setter
    def data(self, value):

    def detach(self):
    @property
    def shape(self):
    @property
    def dtype(self):
    @property
    def device(self):
    def backward(self, out_grad=None):
    
    ...重载运算符...

注意 detach 函数：

def detach(self):
        """Create a new tensor that shares the data but detaches from the graph."""
        return Tensor.make_const(self.realize_cached_data())
    
def make_const(data, requires_grad=False):
        tensor = Tensor.__new__(Tensor)
        tensor._init(
            None,
            [], # 将前置节点置空
            cached_data=data
            if not isinstance(data, Tensor)
            else data.realize_cached_data(),
            requires_grad=requires_grad,
        )
        return tensor

这个函数很有用，它能把节点从计算图剥离出来，防止无效地增加计算图规模（比如梯度下降法更新权重矩阵时）

make_from_op 函数：

def make_from_op(op: Op, inputs: List["Value"]):
        tensor = Tensor.__new__(Tensor)
        tensor._init(op, inputs)
        if not LAZY_MODE:
            tensor.realize_cached_data()
        return tensor

它通过运算操作，和两个输入节点，生成一个新的节点，这个节点的 inputs 就是这两个输入节点，从而将其加入计算图中
LAZY_MODE 的作用可以定义在图建好后再计算

运算操作类实现

对于 Tensor 之间的运算，每次运算都应创建一个新的计算图节点并将它加入计算图中，因此定义 TersorOp 作为 Op 的一个子类：

class TensorOp(Op):
    """ Op class specialized to output tensors, will be alternate subclasses for other structures """

    def __call__(self, *args):
        return Tensor.make_from_op(self, args)

它重写了 __call__ 函数，这个函数委托 Tensor 中的 make_from_op 函数创建一个新的计算图节点 Tensor，通过它就能追踪 Tensor 之间的运算。

接下来对于每一种运算，它都要继承自 Tensor 我们都要重写 compute 函数和 gradient 函数

class EWiseAdd(TensorOp):   # 加
class AddScalar(TensorOp):	# 加常数
class EWiseMul(TensorOp):	# 对应元素乘
class MulScalar(TensorOp):  # 乘常数
class PowerScalar(TensorOp):# 常数幂
class EWiseDiv(TensorOp):   # 对应元素除
class DivScalar(TensorOp):  # 除以常数
class Transpose(TensorOp):  # 颠倒维度
class Reshape(TensorOp):    # 变形
class BroadcastTo(TensorOp):# 广播
class Summation(TensorOp):  # 维度求和
class MatMul(TensorOp):     # 点乘
class Negate(TensorOp):     # 求相反数
class Log(TensorOp):
class Exp(TensorOp):

本文中实现上述操作所需要的矩阵运算我们都使用 numpy 来进行，通过 import numpy as array_api，后续我们将自己实现这些运算，到时候只需要将 numpy 换为自己的 api 即可

计算图 de 建立

考虑如下操作会发生什么：

x = ndl.Tensor([1, 2, 3], dtype="float32")
y = x + 1

当运行 y+1 时，会调用 Tensor 中重载的 __add__ 函数：

def __add__(self, other):
	if isinstance(other, Tensor):
		return needle.ops.EWiseAdd()(self, other)
	else:
		return needle.ops.AddScalar(other)(self)

它判断相加的是常数还是另一个张量，并委托调用相应的 TensorOp 的子类的构造函数，也就是我们前面实现的具体操作类。
而前面提到的 TensorOp 有一个 __call__ 函数，此时它会调用 make_from_op，把当前运算操作类和 inputs 传进去，生成新的计算图节点

由此我们就实现了张量运算的跟踪

自动求导实现

当调用 Tensor 中的 backward 函数时，我们就期望得到每个节点的梯度：

def backward(self, out_grad=None):
    # 最后一个节点时，out_grad为1
	out_grad = out_grad if out_grad else Tensor(numpy.ones(self.shape))
	compute_gradient_of_variables(self, out_grad)

实现我们之前讲解的反向模式算法即可：

def compute_gradient_of_variables(output_tensor, out_grad):
    """Take gradient of output node with respect to each node in node_list.

    Store the computed result in the grad field of each Variable.
    """
    # a map from node to a list of gradient contributions from each output node
    node_to_output_grads_list: Dict[Tensor, List[Tensor]] = {}
    # Special note on initializing gradient of
    # We are really taking a derivative of the scalar reduce_sum(output_node)
    # instead of the vector output_node. But this is the common case for loss function.
    node_to_output_grads_list[output_tensor] = [out_grad]

    # Traverse graph in reverse topological order given the output_node that we are taking gradient wrt.
    reverse_topo_order = list(reversed(find_topo_sort([output_tensor])))

    for node in reverse_topo_order:
      node.grad = sum(node_to_output_grads_list[node])
      if node.is_leaf():
        continue
      for i, grad in enumerate(node.op.gradient_as_tuple(node.grad, node)):
          j =  node.inputs[i]
          if j not in node_to_output_grads_list:
              node_to_output_grads_list[j] = []
          node_to_output_grads_list[j].append(grad)

gradient_as_tuple 函数调用相应运算操作类重写的 gradient 函数计算输入节点的梯度

完整代码

见我的 Github 仓库：

Deconx/CMU-DL-Systems: CMU 10-714 Deep Learning Systems 2022 秋季学期课程作业实现 (github.com)