Note1- 信息检索模型

信息检索模型是一个四元组 $[D, Q, F, R (q_{i}, d_{j})]$

布尔模型

布尔模型是一种最简单的信息检索模型，它返回所有满足布尔表达式的文档。

比如，有如下查询：

Which plays of Shakespeare contain the words Brutus and Caesar, but not Calpurnia?

那么对应的查询就是：Brutus AND Caesar AND NOT Calpurnia

于是可以定义词项与文档的关联矩阵，对于每一个词项，如果其在对应的文档出现过，就将该位置设置为 1，如：

那么当我们要求 Brutus AND Caesar AND NOT Calpurnia 时，只需要对 Calpuria 所在的行求反，然后将这三个向量按位“与”，最后得到的向量就标识了哪些文档符合这个条件。

同样是用一组向量来表示文档 $D (t_{1}, t_{2}, \dots, t_{n})$ ， $t$ 指出现在文档中能够代表文档性质的基本语言单位，即检索词。

即不考虑文档中词的顺序的模型。

设 $t f_{t, d}$ 表示词项 $t$ 在文档 $d$ 中出现的次数，那么就可以定义文档和查询之间的匹配程度为：

t f - m a t c h i n g - s c o r e (q, d) = Σ_{t \in q \cap d} (1 + log t f_{t, d})

考虑高频词含有的信息量往往比低频词要少。因此，设 $d f_{t}$ 为词项 $t$ 在文档集合中出现的文档数目，那么就可以定义**倒置文档频率 (IDF)**为：

i d f_{t} = {log}_{10} \frac{N}{d f}

IDF 衡量了一个词的信息量大小。

那么就可以把文档 $d$ 中的一个词项 $t$ 的权值定义为：

w_{t, d} = (1 + log t f_{t, d}) log \frac{N}{d f_{t}}

即：

内积
余弦相似度
Jaccard 系数
- $J a c c a r d S i m (D_{i}, Q) = \frac{Σ_{k = 1}^{t} (d_{i k} q_{k})}{Σ_{k = 1}^{t} d_{i k}^{2} + Σ_{k = 1}^{t} q_{k}^{2} - Σ_{k = 1}^{t} (d_{i k} q_{k})}$

假设相关度 $R_{d, q}$ 是二值的，即 $R_{d, q} = 1$ 表示文档 $d$ 与查询 $q$ 是相关的，我们利用概率模型来估计每篇文档和查询之间的相关性概率，然后对结果进行降序排列：

p (R = 1 | d, q)

p (R = 1 | x, q) = \frac{p (x | R = 1, q) p (R = 1 | q)}{p (x | q)}

定义排序函数：

O (R | \vec{x}, \vec{q}) = \frac{p (R = 1 | \vec{x}, \vec{q})}{p (R = 0 | \vec{x}, \vec{q})} = \frac{\frac{p (R = 1 | \vec{q}) p (\vec{x} | R = 1, \vec{q})}{p (\vec{x} | \vec{q})}}{\frac{p (R = 0 | \vec{q}) p (\vec{x} | R = 0, \vec{q})}{p (\vec{x} | \vec{q})}} = \frac{p (R = 1 | \vec{q})}{p (R = 0 | \vec{q})} \frac{p (\vec{x} | R = 1, \vec{q})}{p (\vec{x} | R = 0, \vec{q})}

根据贝叶斯条件独立性假设，一个词的出现与否，与任意一个其他词出现与否互相独立，故

\frac{p (\vec{x} | R = 1, \vec{q})}{p (\vec{x} | R = 0, \vec{q})} = \prod_{t = 1}^{M} \frac{p (x_{t} | R = 1, \vec{q})}{p (x_{t} | R = 0, \vec{q})}

从而

O (R | \vec{x}, \vec{q}) = O (R | \vec{q}) \cdot \prod_{t, x_{t} = 1} \frac{p (x_{t} = 1 | R = 1, \vec{q})}{p (x_{t} = 1 | R = 0, \vec{q})} \cdot \prod_{t, x_{t} = 0} \frac{p (x_{t} = 0 | R = 1, \vec{q})}{p (x_{t} = 0 | R = 0, \vec{q})}

令

最后的排序函数为：

\begin{aligned} 0 (R | \vec{x}, \vec{q}) & = O (R | \vec{q}) \cdot \prod_{t, x_{t} = q_{t} = 1} \frac{p_{t}}{u_{t}} \cdot \prod_{t, x_{t} = 0, q_{t} = 1} \frac{1 - p_{t}}{1 - u_{t}} \\ = O (R | \vec{q}) \cdot \prod_{t, x_{t} = q_{t} = 1} \frac{p_{t}}{u_{t}} \cdot \prod_{t, x_{t} = q_{t} = 1} \frac{1 - u_{t}}{1 - p_{t}} \cdot \prod_{t, x_{t} = q_{t} = 1} \frac{1 - p_{t}}{1 - u_{t}} \prod_{t, x_{t} = 0, q_{t} = 1} \frac{1 - p_{t}}{1 - u_{t}} \\ = O (R | \vec{q}) \cdot \prod_{t : x_{t} = q_{t} = 1} \frac{p_{t} (1 - u_{t})}{u_{t} (1 - p_{t})} \cdot \prod_{t : q_{t} = 1} \frac{1 - p_{t}}{1 - u_{t}} \end{aligned}

最终，就得到了我们的检索状态值

R S V_{d} = \log \prod_{t : x_{t} = q_{t} = 1} \frac{p_{t} (1 - u_{t})}{u_{t} (1 - p_{t})} = \sum_{t : x_{t} = q_{t} = 1} \log \frac{p_{t} (1 - u_{t})}{u_{t} (1 - p_{t})}

令 $c_{t} = \log \frac{p_{t} (1 - u_{t})}{u_{t} (1 - p_{t})} = \log \frac{p_{t}}{1 - p_{t}} + \log \frac{1 - u_{t}}{u_{t}}$

举例，假设有如下统计信息：

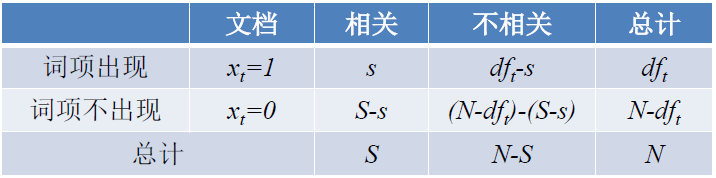
则

c_{t} = \log \frac{p_{t} (1 - u_{t})}{u_{t} (1 - p_{t})} = \log \frac{\frac{s}{(S - s)}}{\frac{(d f_{t} - s)}{((N - d f_{t}) - (S - s))}} = \log \frac{\frac{s + 0.5}{(S - s + 0.5)}}{\frac{(d f_{t} - s + 0.5)}{((N - d f_{t} + s + 0.5) - (S - s + 0.5))}}

\begin{array}{r} R S V_{d} = \sum_{t \in q} \log [\frac{N}{d f_{t}}] \cdot \frac{(k_{1} + 1) t f_{t d}}{k_{1} ((1 - b) + b \times (L_{d} / L_{a v e})) + t f_{t d}} \cdot \frac{(k_{3} + 1) t f_{t q}}{k_{3} + t f_{t q}} \end{array}

文档集中的每篇文档 $d$ 构建其对应的语言模型 $M_{d}$ ，我们的目标是将文档按照其与查询相关的似然 $p (d | q)$ 排序

P (d | q) = \frac{P (q | d) P (d)}{P (q)}

P (q | M_{d}) = P ((t_{1}, t_{2}, \dots, t_{| q |}) | M_{d}) = \prod_{1 \leq k \leq | q |} P (t_{k} | M_{d}) = \prod_{d i s t i n c t t e r m \tan q} P (t | M_{d})^{t f_{d}}

这样估计 $P (t | M_{d})$ ：

\hat{P} (t | M_{d}) = \frac{t f_{t, d}}{| d |}

如果一个词在查询中出现了，但在文档中没有出现，那么 $\prod P (t | M_{d}) = 0$ ，这很不合理。于是就需要概率平滑。

\hat{P} (t | d) = λ {\hat{P}}_{m l e} (t | M_{d}) + (1 - λ) {\hat{P}}_{m l e} (t | M_{c})

$M_{c}$ 是基于全部文档集构造的语言模型。

这个语言模型公式的本质可以理解为：