Note5- 字符串匹配算法总结

Brute Force 算法

其实就是暴力搜索

Horspool 算法

预先计算出一个按字母顺序索引的表 $d$

• $d[c]$：如果窗口中最后一个字符是 $c$，窗口移动多少位置
  • 设模式长度为 $m$
  • $d[c]=m$，如果 $c$ 不包含在模式的前 $m-1$ 个字符中
  • $d[c]=$ 模式前 $m-1$ 个字符中最右边的 $c$ 到模式最后一个字符的距离

以下内容来自： Horspool 算法-CSDN博客

情况 1：看第一行，模式中不存在 c（此时 c 就是字母 A），模式的移动长度就是它的全部长度，移到第二行所示的位置。

情况 2：看第二行，c（此时 c 就是字符 O）正好是模式的最后一个字符，但是从右向左比较时，有字符不匹配，比如此时的 A 和 E 不匹配。而且模式中的其他 m-1 个字符也不包含 c。移动的情况类似情况 1，移动的幅度等于模式的全部长度，移到第三行所示的位置。

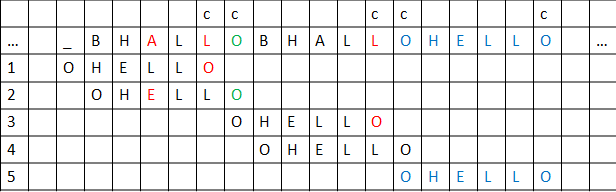
情况 3：看第一行，模式中存在 c（此时 c 就是字符 L），但是它不是模式的最后一个字符，移动时应该把模式中最右边的 c 和文本中的 c 对齐，移到第二行所示的位置。

情况 4：看第二行，c（此时 c 就是字符 O）正好是模式的最后一个字符，但是从右向左比较时，有字符不匹配，比如此时的 A 和 E 不匹配。而此时模式中的其他 m-1 个字符包含 c。移动的情况类似情况 3，移动时应该把前 m-1 个字符中最右边的 c 和文本中的 c 对齐，移到第三行所示的位置。

KMP 算法

学过无数遍的东西了，跳过

Boyer-Moore 算法

以下内容来自：不用找了，学习BM算法，这篇就够了（思路+详注代码）

BM 算法定义了两个规则：

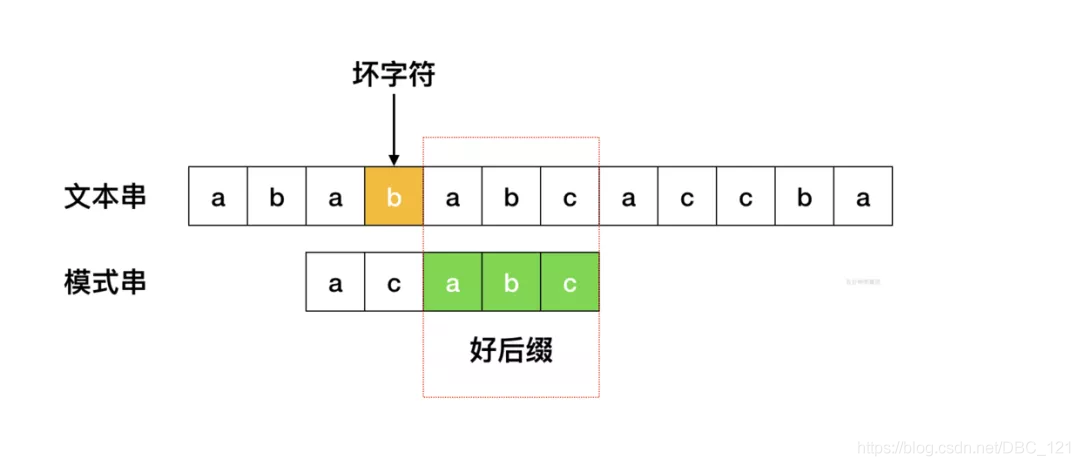
• 坏字符规则：当文本串中的某个字符跟模式串的某个字符不匹配时，我们称文本串中的这个失配字符为坏字符，此时模式串需要向右移动，移动的位数 = 坏字符在模式串中的位置 - 坏字符在模式串中最右出现的位置。此外，如果坏字符不包含在模式串之中，则最右出现位置为 -1。
• 好后缀规则：当字符失配时，后移位数 = 好后缀在模式串中的位置 - 好后缀在模式串上一次出现的位置，且如果好后缀在模式串中没有再次出现，则为 -1。

举例

下面举例说明 BM 算法。例如，给定文本串 HERE IS A SIMPLE EXAMPLE，和模式串 EXAMPLE，现要查找模式串是否在文本串中，如果存在，返回模式串在文本串中的位置。

• 首先，文本串与模式串头部对齐，从尾部开始比较。S 与 E 不匹配。这时，S 就被称为坏字符（bad character），即不匹配的字符，它对应着模式串的第 6 位。且 S 不包含在模式串 EXAMPLE 之中（相当于最右出现位置是 -1），这意味着可以把模式串后移 6-(-1)=7 位，从而直接移到 S 的后一位。

  

• 依然从尾部开始比较，发现 P 与 E 不匹配，所以 P 是坏字符。但是，P 包含在模式串 EXAMPLE 之中。因为 P 这个坏字符对应着模式串的第 6 位（从 0 开始编号），且在模式串中的最右出现位置为 4，所以，将模式串后移 6-4=2 位，两个 P 对齐。

  

  

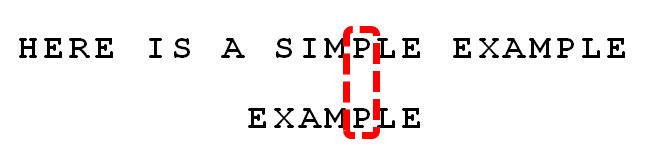
• 依次比较，得到 MPLE 匹配，称为 " 好后缀 "（good suffix），即所有尾部匹配的字符串。注意，"MPLE"、"PLE"、"LE"、"E" 都是好后缀。

  

• 发现 I 与 A 不匹配：I 是坏字符。如果是根据坏字符规则，此时模式串应该后移 2-(-1)=3 位。问题是，有没有更优的移法？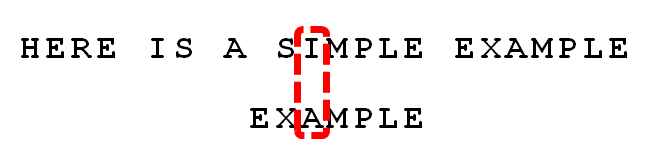

  

  

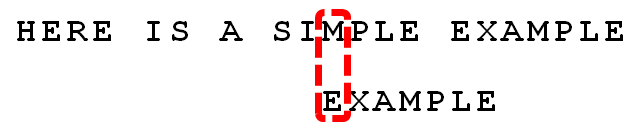
• 更优的移法是利用好后缀规则：当字符失配时，后移位数 = 好后缀在模式串中的位置 - 好后缀在模式串中上一次出现的位置，且如果好后缀在模式串中没有再次出现，则为 -1。所有的好后缀（MPLE、PLE、LE、E）之中，只有 E 在 EXAMPLE 的头部出现，所以后移 6-0=6 位。可以看出，坏字符规则只能移 3 位，好后缀规则可以移 6 位。每次后移这两个规则之中的较大值。这两个规则的移动位数，只与模式串有关，与原文本串无关。

  

• 继续从尾部开始比较，P 与 E 不匹配，因此 P 是坏字符，根据坏字符规则，后移 6 - 4 = 2 位。因为是最后一位就失配，尚未获得好后缀。